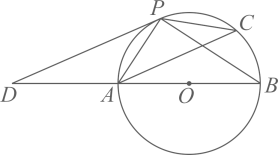
如图，AB是的直径，AC是的一条弦，点P是上一点，且PA=PC ， PD//AC ，与BA的延长线交于点D.

0 返回出卷网首页

1. 如图，AB是 $\text{[math]}$ 的直径，AC是 $\text{[math]}$ 的一条弦，点P是 $\text{[math]}$ 上一点，且PA=PC ， PD//AC ，与BA的延长线交于点D.

(1) 求证：PD是 $\text{[math]}$ 的切线；

(2) 若tan∠PAC= $\text{[math]}$ ，AC = 12.求直径AB的长.

【考点】

平行线的性质; 等腰三角形的性质; 勾股定理; 圆周角定理; 切线的判定;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题普通

1. 如图，点A、B、C、D均在 $\text{[math]}$ 上，直径BC平分 $\text{[math]}$ ， $\text{[math]}$ // $\text{[math]}$ 交BD于点M，延长BD至点N，使得 $\text{[math]}$ ，连接CN.

(1) 求证：CN与 $\text{[math]}$ 相切；

(2) 若 $\text{[math]}$ ， $\text{[math]}$ ，求AB的长.

综合题普通

2. 如图，AB是⊙O的直径，C为⊙O上一点，M是半径OB上动点（不与O、B重合），过点M作EM⊥AB，交BC于点D，交AC的延长线于点E，点F为ED的中点，连接FC.

(1) 求证：FC为⊙O的切线；

(2) 当M为OB的中点时，若CE＝8，CF＝5，求⊙O的半径长.

综合题普通

3. 已知：如图，在△ABC中，BC＝AC，以BC为直径的⊙O与边AB相交于点D，DE⊥AC，垂足为点E.

(1) 求证：点D是AB的中点；

(2) 判断DE与⊙O的位置关系，并证明你的结论；

(3) 若⊙O的直径为10，tanB＝3，求DE的长.

综合题普通