1.
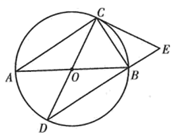
如图,点A、B、C、D均在  上,直径BC平分
上,直径BC平分  ,
, 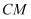 //
//  交BD于点M,延长BD至点N,使得
交BD于点M,延长BD至点N,使得  ,连接CN.
,连接CN.

(1)
求证:CN与  相切;
(2)
若
相切;
(2)
若  ,
,  ,求AB的长.
,求AB的长.
【考点】
等腰三角形的性质;
勾股定理;
圆周角定理;
切线的判定;