0 返回出卷网首页
1. 如图，在等边三角形ABC中，点E是边AC上一定点，点D是直线BC上一动点，以DE为一边作等边三角形DEF，连接CF．

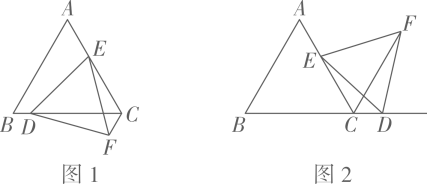
(1) （问题解决）

如图1，若点D在边BC上，求证：CE+CF＝CD；
(2) （类比探究）

如图2，若点D在边BC的延长线上，请探究线段CE，CF与CD之间存在怎样的数量关系？并说明理由．
【考点】
平行线的性质; 三角形全等及其性质; 三角形全等的判定; 等边三角形的性质;
【答案】

您现在未登录，无法查看试题答案与解析。 登录
综合题 困难
能力提升
换一批
1. ∆ABC中，点D在直线AB上.点E在平面内，点F在BC的延长线上，∠E=∠BDC，AE=CD，∠EAB+∠DCF=180º．

(1) 如图①，求证AD+BC=BE；
(2) 如图②、图③，请分别写出线段AD，BC，BE之间的数量关系，不需要证明；
(3) 若BE⊥BC，tan∠BCD= ，CD=10，则AD=．
综合题 困难
2. 如图，在▱ABCD中，点E，F在对角线AC上，且AE=CF．求证：

(1) DE=BF；
(2) 四边形DEBF是平行四边形．
综合题 普通
3. 如图，等边三角形ABC中，点D、E、F、分别为边AB，AC，BC的中点，M为直线BC动点，△DMN为等边三角形

(1) 如图1，当点M在点B左侧时，请你判断EN与MF有怎样的数量关系？
(2) 如图2，当点M在BC上时，其它条件不变，（1）的结论中EN与MF的数量关系是否仍然成立？若成立，请利用图2证明；若不成立请说明理由；
(3) 若点M在点C右侧时，请你在图3中画出相应的图形，并判断（1）的结论是否仍然成立？若成立，请直接写出结论，若不成立请说明理由．
综合题 普通