1.
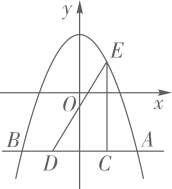
如图,抛物线y=﹣ x2+bx+c与x轴交于点A和点B,与y轴交于点C,点B坐标为(6,0),点C坐标为(0,6),点D是抛物线的顶点,过点D作x轴的垂线,垂足为E,连接BD.

(Ⅰ)求抛物线的解析式及点D的坐标;
(Ⅱ)点F是抛物线上的动点,当∠FBA=∠BDE时,求点F的坐标;
(Ⅲ)若点M是抛物线上的动点,过点M作MN∥x轴与抛物线交于点N,点P在x轴上,点Q在坐标平面内,以线段MN为对角线作正方形MPNQ,请写出点Q的坐标.
【考点】
待定系数法求二次函数解析式;
二次函数图象与坐标轴的交点问题;
相似三角形的判定与性质;
二次函数的实际应用-几何问题;
基础巩固
能力提升
变式训练
拓展培优