1.
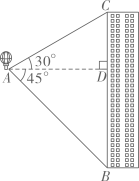
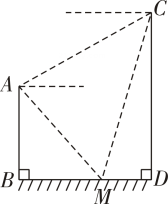
如图,  ,CD为两个建筑物,两建筑物底部之间的水平地面上有一点
,CD为两个建筑物,两建筑物底部之间的水平地面上有一点  .从建筑物
.从建筑物  的顶点
的顶点  测得
测得  点的俯角为45°,从建筑物
点的俯角为45°,从建筑物  的顶点
的顶点  测得
测得  点的俯角为75°,测得建筑物
点的俯角为75°,测得建筑物  的顶点
的顶点  的俯角为30°.若已知建筑物
的俯角为30°.若已知建筑物  的高度为20米,求两建筑物顶点
的高度为20米,求两建筑物顶点  、
、  之间的距离(结果精确到
之间的距离(结果精确到  ,参考数据:
,参考数据:  ,
,  )
)
【考点】
平行线的性质;
锐角三角函数的定义;
解直角三角形的实际应用﹣仰角俯角问题;
等腰直角三角形;