0 返回出卷网首页
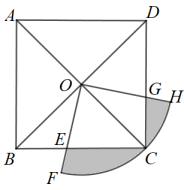
1. 如图，点M，N分别是正方形ABCD的边BC，CD上的点，且BM＝CN， AM与BN交于点P，试探索AM与BN的关系.

(1) 数量关系，并证明；
(2) 位置关系，并证明.
【考点】
正方形的性质; 三角形全等的判定-SAS;
【答案】

您现在未登录，无法查看试题答案与解析。 登录
综合题 普通
能力提升
真题演练
换一批
1. 在正方形ABCD中，AC为对角线，E为AC上一点，连接EB、ED.

(1) 求证：△BEC≌△DEC；
(2) 延长BE交AD于F，当∠BED＝120°时，求∠EFD的度数.
综合题 普通
2. 如图，在正方形ABCD中，点P是对角线AC上一点，连接PB、PD，点E在BC的延长线上，且PE＝PB．

求证：

(1) △BCP ≌△DCP；
(2) ∠DPE ＝∠ABC．
综合题 普通
3. 已知，在△ABC中，∠BAC＝90°，∠ABC＝45°，点D为直线BC上一动点(点D不与点B，C重合)．以AD为边作正方形ADEF，连接CF．

(1) 如图①，当点D在线段BC上时，求证：CF＋CD＝BC；
(2) 如图②，当点D在线段BC的延长线上时，其他条件不变，请写出CF，BC，CD三条线段之间的关系．
综合题 普通