1.
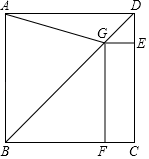
如图1,在正方形ABCD中,E,F分别是BC,CD边上的点(点E不与点B,C重合),且 .
.

(1)
当 时,求证:
时,求证: ;
(2)
猜想BE,EF,DF三条线段之间存在的数量关系,并证明你的结论;
(3)
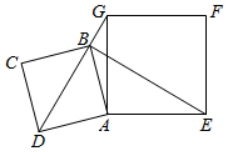
如图2,连接AC,G是CB延长线上一点,
;
(2)
猜想BE,EF,DF三条线段之间存在的数量关系,并证明你的结论;
(3)
如图2,连接AC,G是CB延长线上一点, , 垂足为K,交AC于点H且
, 垂足为K,交AC于点H且 . 若
. 若 ,
,  , 请用含a,b的代数式表示EF的长.
, 请用含a,b的代数式表示EF的长.
【考点】
正方形的性质;
解直角三角形;
三角形全等的判定-SAS;
三角形全等的判定-AAS;