1.
综合与实践
背景阅读:旋转就是将图形上的每一点在平面内绕着旋转中心旋转固定角度的位置移动,其中“旋”是过程,“转”是结果.旋转作为图形变换的一种,具备图形旋转前后对应点到旋转中心的距离相等:对应点与旋转中心所连线段的夹角等于旋转角:旋转前、后的图形是全等图形等性质.所以充分运用这些性质是在解决有关旋转问题的关健.
实践操作:如图1,在Rt△ABC中,∠B=90°,BC=2AB=12,点D , E分别是边BC , AC的中点,连接DE , 将△EDC绕点C按顺时针方向旋转,记旋转角为α.
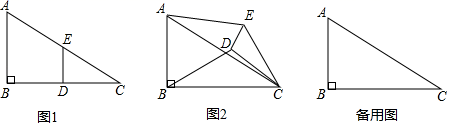
问题解决:
(1)
①当α=0°时,  =;②当α=180°时,
=;②当α=180°时,  =.
(2)
试判断:当0°≤a<360°时,
=.
(2)
试判断:当0°≤a<360°时,  的大小有无变化?请仅就图2的情形给出证明.
(3)
当△EDC旋转至A , D , E三点共线时,求得线段BD的长为.
的大小有无变化?请仅就图2的情形给出证明.
(3)
当△EDC旋转至A , D , E三点共线时,求得线段BD的长为.
【考点】
相似三角形的判定与性质;
旋转的性质;
三角形的中位线定理;
能力提升