1.
如图,在  中,
中,  ,
,  为角平分线.
为角平分线.
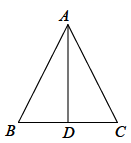
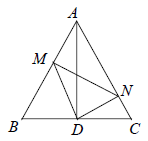
图1 图2
(1)
如图1,已知  ,
,  .求
.求  的面积;
(2)
在(1)的条件下,
的面积;
(2)
在(1)的条件下,  垂直平分线与
垂直平分线与  交于点
交于点  ,画图并求
,画图并求  的长.
(3)
如图2,若
的长.
(3)
如图2,若  为等边三角形,
为等边三角形,  ,
,  分别为边
分别为边  ,
,  上的动点,且满足
上的动点,且满足  .设
.设  ,
,  ,
,  ,请用等式表示
,请用等式表示  ,
,  ,
,  之间的数量关系,并说明理由.
之间的数量关系,并说明理由.
【考点】
三角形的面积;
线段垂直平分线的性质;
等腰三角形的性质;
勾股定理;
三角形全等的判定-SAS;



