1.
请认真阅读下面的数学探究,并完成所提出的问题.

(1)
探究1:如图1,在边长为  的等边三角形
的等边三角形  中,
中,  是
是  边上任意一点,连接
边上任意一点,连接  ,将
,将  绕点
绕点  按顺时针方向旋转至
按顺时针方向旋转至  处,连接
处,连接  ,求
,求  面积的最小值.
(2)
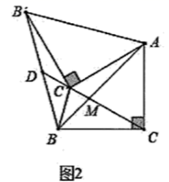
探究2:如图2,若
面积的最小值.
(2)
探究2:如图2,若  是腰长为
是腰长为  的等腰直角三角形,
的等腰直角三角形,  ,(1)中的其他条件不变,请求出此时
,(1)中的其他条件不变,请求出此时  面积的最小值.
(3)
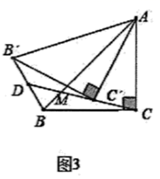
探究3:如图3,在
面积的最小值.
(3)
探究3:如图3,在  中,
中,  ,
,  ,
,  ,
,  是
是  边上任意一点,连接
边上任意一点,连接  ,将
,将  绕点
绕点  按顺时针方向旋转至
按顺时针方向旋转至  处,
处,  、
、  、
、  三点共线,连接
三点共线,连接  ,求
,求  的面积的最小值.
的面积的最小值.
【考点】
等边三角形的判定与性质;
相似三角形的判定与性质;
解直角三角形;
旋转的性质;
等腰直角三角形;
能力提升