1.
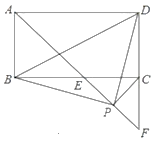
在矩形ABCD中,∠DAB的平分线交BC于点E,交DC的延长线于点F,连接BD.
(1)
计算∠AEC的度数;
(2)
求证:BE=DC;
(3)
点P是线段EF上一动点(不与点E,F重合),在点P运动过程中,能否使△BDP成为等腰直角三角形?若能,写出点P满足的条件并证明;若不能,请说明理由.
【考点】
平行线的性质;
三角形的外角性质;
全等三角形的判定与性质;
等腰三角形的判定与性质;
矩形的性质;