如图，AB是⊙O的直径，BC是⊙O的弦，OD⊥CB于点E，交BC于点E．

0 返回出卷网首页

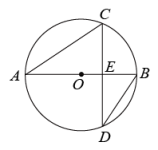
1. 如图，AB是⊙O的直径，BC是⊙O的弦，OD⊥CB于点E，交BC于点E．

(1) 请写出三个不同类型的正确结论；

(2) 连接CD，∠ABC=20°，求∠CDE的度数．

【考点】

垂径定理; 圆周角定理;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题普通

1. 如图，⊙O是△ABC的外接圆，AB是⊙O的直径，D为⊙O上一点，OD⊥AC，垂足为E，连接BD

(1) 求证：BD平分∠ABC；

(2) 当∠ODB=30°时，求证：BC=OD．

综合题普通

2. 如图1，C，D是半圆ACB上的两点，若直径AB上存在一点 $\text{[math]}$ ，确足 $\text{[math]}$ ，则称 $\text{[math]}$ 是 $\text{[math]}$ 的"美丽角".

(1) 如图2，AB是 $\text{[math]}$ 的直径，弦 $\text{[math]}$ 是 $\text{[math]}$ 上一点，连结ED交AB于点 $\text{[math]}$ ，连结 $\text{[math]}$ 是 $\text{[math]}$ 的"美丽角"吗?请说明理由；

(2) 如图3，在(1)的条件下，若直径 $\text{[math]}$ 的"美丽角"为 $\text{[math]}$ ，当DE $\text{[math]}$ 时，求CE的长.

综合题困难

3. 如图，射线PG平分∠EPF，O为射线PG上一点，以O为圆心，10为半径作⊙O，分别与∠EPF两边相交于A、B和C、D，连结OA，此时有OA∥PE

(1) 求证：AP=AO；

(2) 若弦AB=12，求tan∠OPB的值．

综合题普通