1.
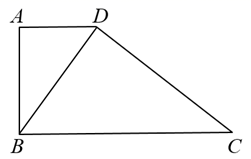
已知:如图,在四边形ABCD中,  ,
,  .
.

(1)
若  ,求出AD,CD,AB之间的数量关系;
(2)
若
,求出AD,CD,AB之间的数量关系;
(2)
若  ,当
,当  于E时,试证明:
于E时,试证明:  ;
(3)
若
;
(3)
若  ,
,  ,
,  ,直接写出AD的长度(用含m的代数式表示).
,直接写出AD的长度(用含m的代数式表示).
【考点】
勾股定理;
相似三角形的判定与性质;
解直角三角形;