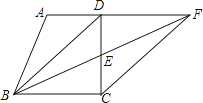
▱ABCD中，对角线AC、BD相交于点O ， E是边AB上的一个动点（不与A、B重合），连接EO并延长，交CD于点F ，连接AF ， CE ，下列四个结论中： ①对于动点E ，四边形AECF始终是平行四边形； ②若∠ABC＜90°，则至少存在一个点E ，使得四边形AECF是矩形； ③若AB＞AD ，则至少存在一个点E ，使得四边形AECF是菱形； ④若∠BAC＝45°，则至少存在一个点E ，使得四边形AECF是正方形．以上所有正确说法的序号是．

1. 在四边形ABCD中，AB＝CD，请添加一个条件，使得四边形ABCD是平行四边形.

填空题容易

如图，四边形ABCD中，AD∥BC，E是DC上一点，连接BE并延长交AD延长线于点F，请你只添加一个条件：使得四边形BDFC为平行四边形．

填空题容易

判定	两组对边	两组对边的四边形是平行四边形
	两组对边	两组对边的四边形是平行四边形
	一组对边	一组对边的四边形是平行四边形
	两条对角线	对角线的四边形是平行四边形

基础知识填空容易

1. 如图，点 $\text{[math]}$ 分别是 $\text{[math]}$ 三边的中点，连结 $\text{[math]}$ ，有下列结论：

①四边形 $\text{[math]}$ 一定是平行四边形；

②若 $\text{[math]}$ ，则四边形 $\text{[math]}$ 是矩形；

③若 $\text{[math]}$ 平分 $\text{[math]}$ ，则四边形 $\text{[math]}$ 是正方形；

④若 $\text{[math]}$ ，则四边形 $\text{[math]}$ 是菱形．

其中正确的有(填序号)

填空题普通

2. 如图，在四边形ABCD中，对角线AC，BD交于点O，OA=OC，OB=OD，添加一个条件使四边形ABCD是菱形，那么所添加的条件可以是（写出一个即可）．

填空题普通

3. 如图，在四边形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，在不添加任何辅助线的前提下，要想四边形 $\text{[math]}$ 成为一个矩形，只需添加的一个条件是.

填空题普通

1. 下列命题中，真命题是（）

A. 一组对边平行的四边形是平行四边形 B. 对角线相等的平行四边形是矩形 C. 对角线互相垂直四边形是菱形 D. 四边相等的四边形是正方形

单选题容易

2. 下面结论中，正确的是（）．

A. 对角线相等的四边形是矩形 B. 对角线互相平分的四边形是平行四边形 C. 对角线互相垂直的四边形是菱形 D. 对角线互相垂直且相等的四边形是正方形

单选题普通

3. 下列说法错误的是（）

A. 对角线互相平分的四边形是平行四边形 B. 四个角都相等的四边形是矩形 C. 四条边都相等的四边形是菱形 D. 对角线垂直且相等的四边形是正方形

单选题普通

1. 已知：如图，四边形ABCD四条边上的中点分别为E、F、G、H，顺次连接EF、FG、GH、HE，得到四边形EFGH(即四边形ABCD的中点四边形).

(1) 四边形EFGH的形状是 ▲ ，并证明你的结论.

(2) 当AC、BD满足时，四边形EFGH是菱形.

(3) 当AC、BD满足时，四边形EFGH是矩形.

(4) 当AC、BD满足时，四边形EFGH是正方形.

综合题普通

2. 如图，将 $\text{[math]}$ 沿线段 $\text{[math]}$ 向右平移得到 $\text{[math]}$ ，此时 $\text{[math]}$ ，连接 $\text{[math]}$ ．

(1) 求证：四边形 $\text{[math]}$ 是平行四边形；

(2) ①若 $\text{[math]}$ ，求证：四边形 $\text{[math]}$ 是菱形；

②若 $\text{[math]}$ ，求证：四边形 $\text{[math]}$ 是矩形；

③若 $\text{[math]}$ ， $\text{[math]}$ ，求证：四边形 $\text{[math]}$ 是正方形．

综合题普通

3. 如图，在△ABC中，D是AB中点，E是AC中点，F是BC中点，请填空：

(1) 四边形BDEF是四边形；

(2) 若四边形BDEF是菱形，则△ABC满足的条件是.

(3) 若四边形BDEF是矩形，则△ABC满足的条件是.

(4) 若四边形BDEF是正方形，则△ABC满足的条件是.并就（2）、（3）、（4）中选取一个进行证明.

填空题普通

1. 下列命题：

①一组对边平行，另一组对边相等的四边形是平行四边形；②对角线互相垂直且平分的四边形是菱形；③一个角为90°且一组邻边相等的四边形是正方形；④对角线相等的平行四边形是矩形．其中真命题的个数是（）

A. 1 B. 2 C. 3 D. 4

单选题普通

2. 下列命题，其中是真命题的是（）

A. 对角线互相垂直的四边形是平行四边形 B. 有一个角是直角的四边形是矩形 C. 对角线互相平分的四边形是菱形 D. 对角线互相垂直的矩形是正方形

单选题普通

3. 下列命题，其中是真命题的为（）

A. 一组对边平行，另一组对边相等的四边形是平行四边形 B. 对角线互相垂直的四边形是菱形 C. 对角线相等的四边形是矩形 D. 一组邻边相等的矩形是正方形

单选题容易