0 返回出卷网首页
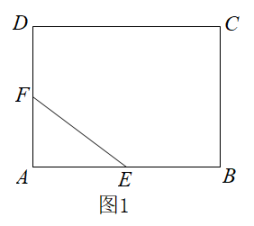
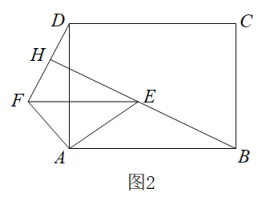
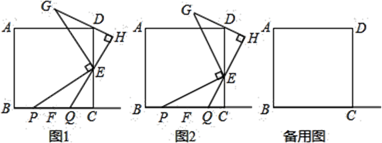
1. 如图，四边形ABCD是正方形，E是AD上任意一点，延长BA到F，使得AF=AE，连接DF：

(1) 旋转△ADF可得到哪个三角形？
(2) 旋转中心是哪一点？旋转了多少度？
(3) BE与DF的数量关系、位置关系如何？为什么？
【考点】
旋转的性质;
【答案】

您现在未登录，无法查看试题答案与解析。 登录
综合题 普通
能力提升
真题演练
换一批
1. 把两个三角形按如图1放置，其中∠ACB=∠DEC=90°，∠CAB=45°，∠CDE=30°，且AB=6，DC=7，把△DCE绕点C顺时针旋转15°得△D1CE1 ， 如图2，这时AB与CD1相交于点O，与D1E1相交于点F．

(1) 求∠ACD1的度数；
(2) 求线段AD1的长．
综合题 普通
2. 在△ABC中，AB=BC=2，∠ABC=120°，将△ABC绕点B顺时针旋转角α（0°＜α＜90°）得△A1BC1 ， A1B交AC于点E，A1C1分别交AC、BC于D、F两点．
(1) 如图1，观察并猜想，在旋转过程中，线段BE与BF有怎样的数量关系？并证明你的结论；

(2) 如图2，当α=30°时，试判断四边形BC1DA的形状，并说明理由．

综合题 普通
3. 如图①，在Rt△ABC中，∠C=90°．将△ABC绕点C逆时针旋转得到△A′B′C，旋转角为α，且0°＜α＜180°．在旋转过程中，点B′可以恰好落在AB的中点处，如图②．

(1) 求∠A的度数；
(2) 当点C到AA′的距离等于AC的一半时，求α的度数．
综合题 普通