如图1，在平面直角坐标系xOy中，点A的坐标为（0，1），取一点B（b，0），连接AB，做线段AB的垂直平分线l1 ，过点B作x轴的垂线l2 ，记l1 ， l2的交点为P．

0 返回出卷网首页

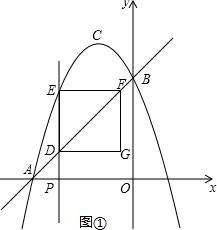
1. 如图1，在平面直角坐标系xOy中，点A的坐标为（0，1），取一点B（b，0），连接AB，做线段AB的垂直平分线l₁ ，过点B作x轴的垂线l₂ ，记l₁ ， l₂的交点为P．

(1) 当b=3时，在图1中补全图形（尺规作图，不写作法，保留作图痕迹）；

(2) 小慧多次取不同数值b，得出相应的点P，并把这些点用平滑的曲线连接起来发现：这些点P竟然在一条曲线L上！

①设点P的坐标为（x，y），试求y与x之间的关系式，并指出曲线L是哪种曲线；

②设点P到x轴，y轴的距离分别是d₁ ， d₂ ，求d₁+d₂的范围，当d₁+d₂=8时，求点P的坐标；

③将曲线L在直线y=2下方的部分沿直线y=2向上翻折，得到一条“W”形状的新曲线，若直线y=kx+3与这条“W”形状的新曲线有4个交点，直接写出k的取值范围．

【考点】

勾股定理; 二次函数与一次函数的综合应用;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题困难

1. 如图，“爱心”图案是由抛物线 $\text{[math]}$ 的一部分及其关于直线y＝x的对称图形组成，点A、B是“爱心”图案与其对称轴的两个交点，点C、D、E、F是图案与坐标轴的交点，且点C的坐标为 $\text{[math]}$ .

(1) 求k的值及DF的长.

(2) 求AB的长.

综合题普通

2. 如图，抛物线 $\text{[math]}$ 交 $\text{[math]}$ 轴于点 $\text{[math]}$ ，交 $\text{[math]}$ 轴于点 $\text{[math]}$ ，已知经过点 $\text{[math]}$ ， $\text{[math]}$ 的直线的表达式为 $\text{[math]}$ ．

(1) 求抛物线的函数表达式及其顶点 $\text{[math]}$ 的坐标；

(2) 如图 $\text{[math]}$ ，点 $\text{[math]}$ 是线段 $\text{[math]}$ 上的一个动点，其中 $\text{[math]}$ ，作直线 $\text{[math]}$ 轴，交直线 $\text{[math]}$ 于 $\text{[math]}$ ，交抛物线于 $\text{[math]}$ ，作 $\text{[math]}$ 轴，交直线 $\text{[math]}$ 于点 $\text{[math]}$ ，四边形 $\text{[math]}$ 为矩形．设矩形 $\text{[math]}$ 的周长为 $\text{[math]}$ ，写出 $\text{[math]}$ 与 $\text{[math]}$ 的函数关系式，并求 $\text{[math]}$ 为何值时周长 $\text{[math]}$ 最大；

(3) 如图 $\text{[math]}$ ，在抛物线的对称轴上是否存在点 $\text{[math]}$ ，使点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 构成的三角形是以 $\text{[math]}$ 为腰的等腰三角形？若存在，直接写出所有符合条件的点 $\text{[math]}$ 的坐标；若不存在，请说明理由．

综合题困难

3. 如图，在Rt△ABC中，∠ACB=90°，AC=8，BC=6，Q为AB的中点．动点P从点A出发沿折线AC--CB以每秒2个单位长度的速度运动，连结PQ，以PQ为边构造正方形PMNQ且边MN与点B始终在边PQ同侧．设点P的运动时间为t秒(>0)．

(1) 线段AB的长为

(2) 当点P在边AC上运动时，线段CP的长为 ▲ (用含t的代数式表示) ．

①当正方形PMNQ与△ABC重叠部分图形是正方形时，求t的取值范围．

②当边MN的中点落在△ABC的边上时，求正方形PMNQ的面积．

(3) 当点P不与点C重合时，作点C关于直线PQ的对称点C'当PC'⊥AB时，直接写出t的值．

综合题普通