1.
如图,抛物线 交
交 轴于点
轴于点 , 交
, 交 轴于点
轴于点 , 已知经过点
, 已知经过点 ,
,  的直线的表达式为
的直线的表达式为 .
.
(1)
求抛物线的函数表达式及其顶点 的坐标;
(2)
如图
的坐标;
(2)
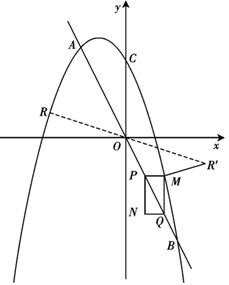
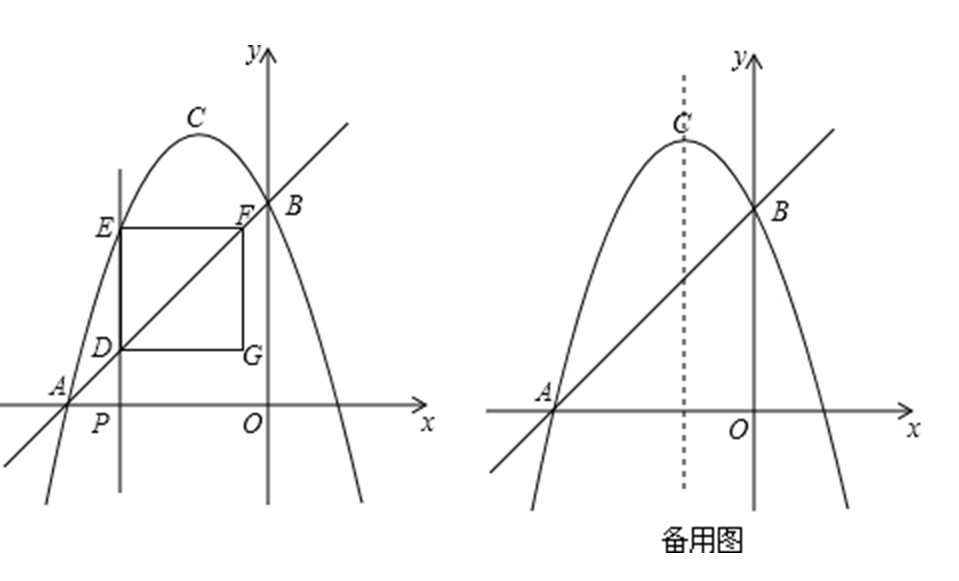
如图 , 点
, 点 是线段
是线段 上的一个动点,其中
上的一个动点,其中 , 作直线
, 作直线 轴,交直线
轴,交直线 于
于 , 交抛物线于
, 交抛物线于 , 作
, 作 轴,交直线
轴,交直线 于点
于点 , 四边形
, 四边形 为矩形.设矩形
为矩形.设矩形 的周长为
的周长为 , 写出
, 写出 与
与 的函数关系式,并求
的函数关系式,并求 为何值时周长
为何值时周长 最大;
(3)
如图
最大;
(3)
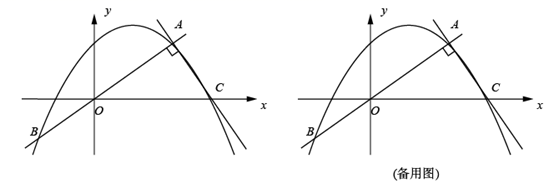
如图 , 在抛物线的对称轴上是否存在点
, 在抛物线的对称轴上是否存在点 , 使点
, 使点 ,
,  ,
,  构成的三角形是以
构成的三角形是以 为腰的等腰三角形?若存在,直接写出所有符合条件的点
为腰的等腰三角形?若存在,直接写出所有符合条件的点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
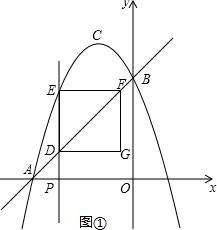
【考点】
勾股定理;
二次函数与一次函数的综合应用;
能力提升
真题演练