1.
老师在上课时,在黑板上写了一道题:
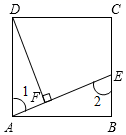
“如图,ABCD是正方形,点E在BC上,DF⊥AE于F,请问图中是否存在一组全等三角形?”
小杰同学经过思考发现:△ADF≌△EAB.
理由如下:因为ABCD是正方形(已知)
所以∠B=90°且AD=AB和AD∥BC
又因为DF⊥AE(已知)
即∠DFA=90°(垂直的意义)
所以∠DFA=∠B(等量代换)
又AD∥BC
所以∠1=∠2(两直线平行,内错角相等)
在△ADF和△EAB中
所以△ADF≌△EAB(AAS)
小胖却说这题是错误的,这两个三角形根本不全等.
你知道小杰的错误原因是什么吗?我们再添加一条线段,就能找到与△ADF全等的三角形,请能说出此线段的做法吗?并说明理由.
【考点】
正方形的性质;
三角形全等的判定-AAS;
基础巩固
能力提升
变式训练
拓展培优
真题演练