1.
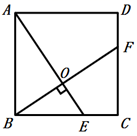
如图，在正方形ABCD中，点E是BC边上的动点，连接AE，过点 B 作BH⊥AE，交AE 于点 G，交 CD 于点 F，过点 D 作 DH⊥BH 于点 H.
(1)
如图①，当点E是BC中点时，若AB=6， 
求FH的长；
(2)
如图②，连接HC，当点 E 在 BC 边上运动时，试判断FH，EG，BG之间的数量关系，并说明理由.
【考点】
勾股定理;
正方形的性质;
三角形全等的判定-ASA;
三角形全等的判定-AAS;
正方形中的十字架模型;
相似三角形的判定-AA;
