1.
平面直角坐标系xOy中,对于任意的三个点A、B、C,给出如下定义:若矩形的任何一条边均与某条坐标轴平行,且A,B,C三点都在矩形的内部或边界上,则称该矩形为点A,B,C的“三点矩形”.在点A,B,C的所有“三点矩形”中,若存在面积最小的矩形,则称该矩形为点A,B,C的“最佳三点矩形”.
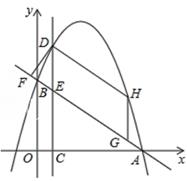
如图1,矩形DEFG,矩形IJCH都是点A,B,C的“三点矩形”,矩形IJCH是点A,B,C的“最佳三点矩形”.
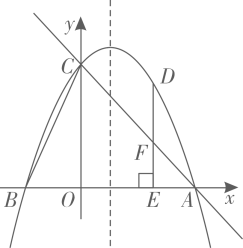
如图2,已知M(4,1),N(﹣2,3),点P(m,n).

(1)
①若m=1,n=4,求点M,N,P的“最佳三点矩形”的周长和面积;
(2)
若点P在直线y=﹣2x+4上.
(3)
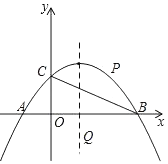
若点P(m,n)在抛物线y=ax2+bx+c上,且当点M,N,P的“最佳三点矩形”面积为12时,﹣2≤m≤﹣1或1≤m≤3,直接写出抛物线的解析式.
②若m=1,点M,N,P的“最佳三点矩形”的面积为24,求n的值;
①求点M,N,P的“最佳三点矩形”面积的最小值及此时m的取值范围;
②当点M,N,P的“最佳三点矩形”为正方形时,求点P的坐标;
【考点】
二次函数的实际应用-几何问题;
能力提升
真题演练