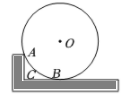
如图，王老师将汽车停放放置在地面台阶直角处，他测量了台阶高为，汽车轮胎的直径为，请你计算直角顶点到轮胎与底面接触点长为（）.

0 返回出卷网首页

1. 如图，王老师将汽车停放放置在地面台阶直角处，他测量了台阶高 $\text{[math]}$ 为 $\text{[math]}$ ，汽车轮胎的直径为 $\text{[math]}$ ，请你计算直角顶点到轮胎与底面接触点 $\text{[math]}$ 长为（）.

A. $\text{[math]}$ B. $\text{[math]}$ C. $\text{[math]}$ D. $\text{[math]}$

【考点】

勾股定理; 矩形的判定与性质; 切线的性质;

【答案】

您现在未登录，无法查看试题答案与解析。登录

单选题普通

1. 如图，P为⊙O外一点，PC切⊙O于C，PB与⊙O交于A、B两点.若PA＝1，PB＝5，则PC＝（）

A. 3 B. $\text{[math]}$ C. 4 D. 无法确定

单选题容易

2. 如图，AB与 $\text{[math]}$ 相切于点 $\text{[math]}$ ，若 $\text{[math]}$ 的半径为 $\text{[math]}$ ，则AO的长为（）

A. $\text{[math]}$ B. $\text{[math]}$ C. $\text{[math]}$ D. 4

单选题容易

3. 如图， $\text{[math]}$ 与 $\text{[math]}$ 相切于点 $\text{[math]}$ ，若 $\text{[math]}$ 的半径为 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的长为（）

A. $\text{[math]}$ B. $\text{[math]}$ C. $\text{[math]}$ D. 4

单选题容易