1.
探究：如图1和图2，四边形 
中，已知 
， 
，点 
、 
分别在 
、 
上， 
.
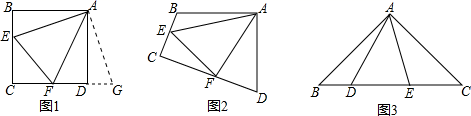
(1)
①如图1，若 
、 
都是直角，把 
绕点 
逆时针旋转90°至 
，使 
与 
重合，直接写出线段 
、 
和 
之间的数量关系 ▲ ；
(2)
拓展：如图3，在 
中， 
， 
，点 
、 均在边 上，且 
，若 
，求 
的长.
②如图2，若 、
都不是直角，但满足
，线段
、
和
之间①中的结论是否仍然成立，若成立，请写出证明过程；若不成立，请说明理由.
【考点】
勾股定理;
旋转的性质;
等腰直角三角形;
三角形全等的判定-SAS;
