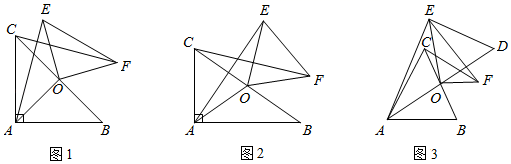
1.
如图,在  中,
中,  ,
,  为
为  边上的点,将
边上的点,将  绕
绕  逆时针旋转
逆时针旋转  得到
得到  .
.

(1)
如图1,若  .
(2)
如图2,
.
(2)
如图2,  为
为  边上任意一点,线段
边上任意一点,线段  、
、  、
、  是否满足(1)中②的关系,请给出结论并证明.
是否满足(1)中②的关系,请给出结论并证明.
①求证: ;
②直接写出 与
的数量关系为 ▲ ;
【考点】
勾股定理;
相似三角形的判定与性质;
旋转的性质;
三角形全等的判定-SAS;
能力提升
真题演练