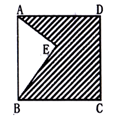
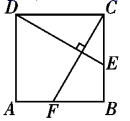
如图，在正方形ABCD中，E为AB中点，连结DE，过点D作交BC的延长线于点F，连结若，则EF的值为

0 返回出卷网首页

1. 如图，在正方形ABCD中，E为AB中点，连结DE，过点D作 $\text{[math]}$ 交BC的延长线于点F，连结 $\text{[math]}$ 若 $\text{[math]}$ ，则EF的值为 $\text{[math]}$ $\text{[math]}$

A. 3 B. $\text{[math]}$ C. $\text{[math]}$ D. 4

【考点】

勾股定理; 正方形的性质; 三角形全等的判定-ASA;

【答案】

您现在未登录，无法查看试题答案与解析。登录

单选题普通

1. 如图，字母 $\text{[math]}$ 所代表的正方形的面积是( )

A. 194 B. 144 C. 13 D. 12

单选题容易

2. 四个全等的直角三角形按图示方式围成正方形 $\text{[math]}$ ，过各较长直角边的中点作垂线，围成面积为S的小正方形 $\text{[math]}$ ．已知 $\text{[math]}$ 为 $\text{[math]}$ 较长直角边，若 $\text{[math]}$ ，则正方形 $\text{[math]}$ 的面积为（）

A. $\text{[math]}$ B. $\text{[math]}$ C. $\text{[math]}$ D. $\text{[math]}$

单选题容易

3. 如图，四边形ABCD是正方形，AE垂直于BE，且AE＝6，BE＝8，则阴影部分的面积是（）

A. 66 B. 76 C. 64 D. 100

单选题容易