1.
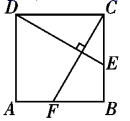
如图,点E为正方形ABCD的边DA的延长线上一点,以BE为边在BE的另一侧作正方形BEFG,连接CG,若AB=12,BE=13,则△BCG的面积为.

【考点】
勾股定理;
正方形的性质;
三角形全等的判定-ASA;