1.
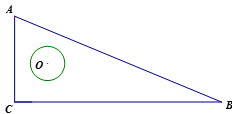
如图,在  中,
中,  ,点
,点  为边
为边  上一动点,连结
上一动点,连结  .以
.以  为圆心,
为圆心,  为半径作圆,交
为半径作圆,交  于
于  ,过
,过  作⊙O的切线,交
作⊙O的切线,交  于点
于点  .当⊙O与边
.当⊙O与边  相切时,
相切时,  的长为.
的长为.

【考点】
切线的性质;
相似三角形的判定与性质;
切线长定理;