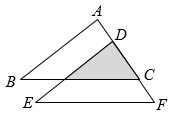
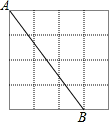
如图，方格纸中每个小正方形的边长均为1，其顶点称为格点．的顶点都在小正方形的格点上．以点A为圆心，适当长为半径画弧，交于点 M，交于点N；分别以点M，N为圆心，大于的长为半径画弧，两弧在的内部相交于点D；画射线交于点P，设．点 Q为线段上的动点，则下列结论：① ；②若分别连接，，则；③当时，；④ 的最小值为m．其中正确的有（）

0 返回出卷网首页

1. 如图，方格纸中每个小正方形的边长均为1，其顶点称为格点． $\text{[math]}$ 的顶点都在小正方形的格点上．以点A为圆心，适当长为半径画弧，交 $\text{[math]}$ 于点 M，交 $\text{[math]}$ 于点N；分别以点M，N为圆心，大于 $\text{[math]}$ 的长为半径画弧，两弧在 $\text{[math]}$ 的内部相交于点D；画射线 $\text{[math]}$ 交 $\text{[math]}$ 于点P，设 $\text{[math]}$ ．点 Q为线段 $\text{[math]}$ 上的动点，则下列结论：① $\text{[math]}$ ；②若分别连接 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ ；③当 $\text{[math]}$ 时， $\text{[math]}$ ；④ $\text{[math]}$ 的最小值为m．其中正确的有（）

A. 1个 B. 2个 C. 3个 D. 4个

【考点】

勾股定理的逆定理; 相似三角形的判定与性质;

【答案】

您现在未登录，无法查看试题答案与解析。登录

单选题困难

1. 一个三角形三边的比是 $\text{[math]}$ ，那么这个三角形是（）

A. 钝角三角形 B. 锐角三角形 C. 直角三角形 D. 不能确定

单选题容易

2. 若a、b、c为三角形三边，则下列各项中不能构成直角三角形的是( )

A. a=7，b=24，c=25 B. a=5，b=13，c=12 C. a=1，b=2，c=3 D. a=30，b=40，c=50

单选题容易

3. 以下列各组数为边长，能组成直角三角形的是( )

A. 8，15，17 B. 4，5，6 C. 5，8，10 D. 8，39，40

单选题容易