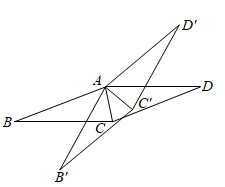
如图.将菱形ABCD绕点A逆时针旋转得到菱形， .当AC平分时，与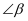满足的数量关系是（）

0 返回出卷网首页

1. 如图.将菱形ABCD绕点A逆时针旋转 $\text{[math]}$ 得到菱形 $\text{[math]}$ ， $\text{[math]}$ .当AC平分 $\text{[math]}$ 时， $\text{[math]}$ 与 $\text{[math]}$ 满足的数量关系是（）

A. $\text{[math]}$ B. $\text{[math]}$ C. $\text{[math]}$ D. $\text{[math]}$

【考点】

等腰三角形的性质; 菱形的性质; 旋转的性质;

【答案】

您现在未登录，无法查看试题答案与解析。登录

单选题普通

1. 如图，AD，CE分别是△ABC的中线和角平分线．若AB=AC，∠CAD=20°，则∠ACE的度数是（）

A. 20° B. 35° C. 40° D. 70°

单选题容易

2. 等腰三角形的一个内角为 $\text{[math]}$ ，则另外两个内角的度数分别是（）

A. $\text{[math]}$ B. $\text{[math]}$ 或 $\text{[math]}$ C. $\text{[math]}$ D. $\text{[math]}$ 或 $\text{[math]}$

单选题容易

3. 方程x²﹣9x+14＝0的两个根分别是等腰三角形的底和腰，则这个三角形的周长为（）

A. 11 B. 16 C. 11或16 D. 不能确定

单选题容易