1.
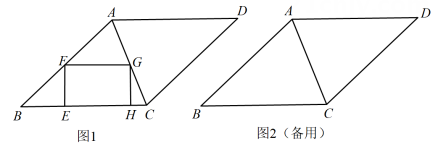
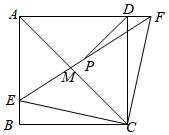
如图,正方形  中,点
中,点  是边
是边  上一动点,点
上一动点,点  在边
在边  的延长线上,且
的延长线上,且  .连接
.连接  ,
,  ,
,  ,
,  ,
,  与
与  交于点
交于点  .
.
(1)
求证:  .
(2)
若
.
(2)
若  ,试求
,试求  的度数.
(3)
设
的度数.
(3)
设  的中点为
的中点为  ,连接
,连接  .在点
.在点  的运动过程中,
的运动过程中,  的值是否会发生变化?若不变,请求出它的值;若变化,请求出它的取值范围.
的值是否会发生变化?若不变,请求出它的值;若变化,请求出它的取值范围.
【考点】
相似三角形的判定与性质;
解直角三角形;
四边形-动点问题;
能力提升
真题演练