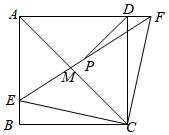
如图，平行四边形ABCD中，DB＝， AB＝4，AD＝2，动点E，F同时从A点出发，点E沿着A→D→B的路线匀速运动，点F沿着A→B→D的路线匀速运动，当点E，F相遇时停止运动．

0 返回出卷网首页

1. 如图，平行四边形ABCD中，DB＝ $\text{[math]}$ ， AB＝4，AD＝2，动点E，F同时从A点出发，点E沿着A→D→B的路线匀速运动，点F沿着A→B→D的路线匀速运动，当点E，F相遇时停止运动．

(1) 如图1，设点E的速度为1个单位每秒，点F的速度为4个单位每秒，当运动时间为 $\text{[math]}$ 秒时，设CE与DF交于点P，求线段EP与CP长度的比值；

(2) 如图2，设点E的速度为1个单位每秒，点F的速度为 $\text{[math]}$ 个单位每秒，运动时间为x秒，ΔAEF的面积为y，求y关于x的函数解析式，并指出当x为何值时，y的值最大，最大值为多少？

(3) 如图3，H在线段AB上且AH＝ $\text{[math]}$ HB，M为DF的中点，当点E、F分别在线段AD、AB上运动时，探究点E、F在什么位置能使EM＝HM．并说明理由．

【考点】

相似三角形的判定与性质; 解直角三角形; 二次函数-动态几何问题; 四边形-动点问题;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题困难

1. 如图，正方形 $\text{[math]}$ 中，点 $\text{[math]}$ 是边 $\text{[math]}$ 上一动点，点 $\text{[math]}$ 在边 $\text{[math]}$ 的延长线上，且 $\text{[math]}$ .连接 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 与 $\text{[math]}$ 交于点 $\text{[math]}$ .

(1) 求证： $\text{[math]}$ .

(2) 若 $\text{[math]}$ ，试求 $\text{[math]}$ 的度数.

(3) 设 $\text{[math]}$ 的中点为 $\text{[math]}$ ，连接 $\text{[math]}$ .在点 $\text{[math]}$ 的运动过程中， $\text{[math]}$ 的值是否会发生变化？若不变，请求出它的值；若变化，请求出它的取值范围.

综合题困难

2. 如图，平面直角坐标系中，矩形OABC的两边分别在x轴和y轴上，OA＝ $\text{[math]}$ cm，OC＝8cm，现有两动点P、Q分别从O、C同时出发，P在线段OA上沿OA方向以每秒 $\text{[math]}$ cm的速度匀速运动，Q在线段CO上沿CO方向以每秒1cm的速度匀速运动．设运动时间为t秒．

(1) 用t的式子表示△OPQ的面积S；

(2) 求证：四边形OPBQ的面积是一个定值，并求出这个定值；

(3) 当△OPQ与△PAB和△QPB相似时，抛物线y＝ $\text{[math]}$ x²＋bx＋c经过B、P两点，过线段BP上一动点M作y轴的平行线交抛物线于N，当线段MN的长取最大值时，求直线MN把四边形OPBQ分成两部分的面积之比．

综合题困难

3. 我们经常会采用不同方法对某物体进行测量，请测量下列灯杆AB的长．

(1) 如图1所示，将一个测角仪放置在距离灯杆AB底部a米的点D处，测角仪高为b米，从C点测得A点的仰角为α，求灯杆AB的高度．（用含a，b，ａ的代数式表示）

(2) 我国古代数学家赵爽利用影子对物体进行测量的方法，在至今仍有借鉴意义图2所示，现将一高度为2米的木杆CG放在灯杆AB前，测得其影长CH为1米，再将木杆沿着BC方向移动1.8米至DE的位置，此时测得其影长DF为3米，求灯杆AB的高度

综合题困难