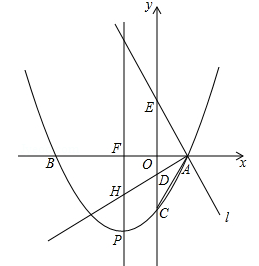
已知，抛物线y＝mx2＋ x﹣4m与x轴交于点A（﹣4，0）和点B ，与y轴交于点C ．点D（n ， 0）为x轴上一动点，且有﹣4＜n＜0，过点D作直线1⊥x轴，且与直线AC交于点M ，与抛物线交于点N ，过点N作NP⊥AC于点P ．点E在第三象限内，且有OE＝OD ．

0 返回出卷网首页

1. 已知，抛物线y＝mx²＋ $\text{[math]}$ x﹣4m与x轴交于点A（﹣4，0）和点B ，与y轴交于点C ．点D（n ， 0）为x轴上一动点，且有﹣4＜n＜0，过点D作直线1⊥x轴，且与直线AC交于点M ，与抛物线交于点N ，过点N作NP⊥AC于点P ．点E在第三象限内，且有OE＝OD ．

(1) 求m的值和直线AC的解析式．

(2) 若点D在运动过程中， $\text{[math]}$ AD＋CD取得最小值时，求此时n的值．

(3) 若点△ADM的周长与△MNP的周长的比为5∶6时，求AE＋ $\text{[math]}$ CE的最小值．

【考点】

待定系数法求一次函数解析式; 相似三角形的判定与性质; 二次函数-动态几何问题;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题困难

1. 如图，在平面直角坐标系xOy中，直线y=kx+b（k≠0）与双曲线y= $\text{[math]}$ 相交于点A（m，6）和点B（﹣3，n），直线AB与y轴交于点C．

(1) 求直线AB的表达式；

(2) 求AC：CB的值．

综合题普通

2. 如图，抛物线y=-x²+mx+2m²（m＞0）与x轴交于A、B两点，点A在点B的左边，C是抛物线上一个动点（点C与点A、B不重合），D是OC的中点，连接BD并延长，交AC于点E．

(1) 用含m的代数式表示点A、B的坐标；

(2) 求证： $\text{[math]}$ ；

(3) 若点C、点A到y轴的距离相等，且s_△CDE=1.6时，求抛物线和直线BE的解析式．

综合题普通

3. 如图，一次函数y=kx+b（k≠0）的图象与x轴，y轴分别交于A（﹣9，0），B（0，6）两点，过点C（2，0）作直线l与BC垂直，点E在直线l位于x轴上方的部分.

(1) 求一次函数y=kx+b（k≠0）的表达式；

(2) 若△ACE的面积为11，求点E的坐标；

(3) 当∠CBE=∠ABO时，点E的坐标为.

综合题普通