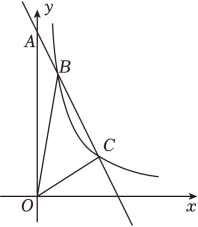
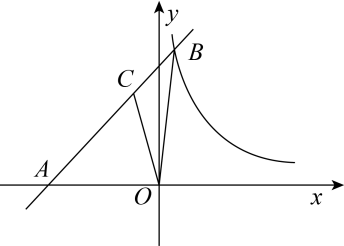
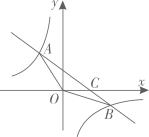
如图，直线与双曲线交于，两点，与轴，轴分别交于，两点，且 .

0 返回出卷网首页

1. 如图，直线 $\text{[math]}$ 与双曲线 $\text{[math]}$ 交于 $\text{[math]}$ ， $\text{[math]}$ 两点，与 $\text{[math]}$ 轴， $\text{[math]}$ 轴分别交于 $\text{[math]}$ ， $\text{[math]}$ 两点，且 $\text{[math]}$ .

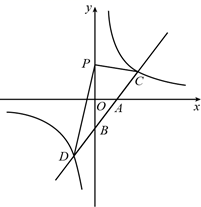
(1) 求一次函数和反比例函数的解析式.

(2) 将点 $\text{[math]}$ 沿 $\text{[math]}$ 轴平移得到点 $\text{[math]}$ ，若 $\text{[math]}$ 的面积为36，求点 $\text{[math]}$ 的坐标.

【考点】

反比例函数与一次函数的交点问题; 三角形的面积; 锐角三角函数的定义;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题普通

1. 如图所示，直线 $\text{[math]}$ 与双曲线 $\text{[math]}$ 交于 $\text{[math]}$ 、 $\text{[math]}$ 两点，已知点 $\text{[math]}$ 的纵坐标为 $\text{[math]}$ ，直线 $\text{[math]}$ 与 $\text{[math]}$ 轴交于点 $\text{[math]}$ ，与 $\text{[math]}$ 轴交于点 $\text{[math]}$ ， $\text{[math]}$ $\text{[math]}$ ， $\text{[math]}$ .

(1) 求直线 $\text{[math]}$ 的解析式；

(2) 若点 $\text{[math]}$ 是第二象限内反比例函数图象上的一点， $\text{[math]}$ 的面积是 $\text{[math]}$ 的面积的 $\text{[math]}$ 倍，求点 $\text{[math]}$ 的坐标；

(3) 直接写出不等式 $\text{[math]}$ 的解集.

综合题普通

2. 如图，一次函数 $\text{[math]}$ 的图象与y轴交于点A ，与反比例函数的图象交于点 $\text{[math]}$ 和点 $\text{[math]}$ ，连接 $\text{[math]}$ ．

(1) 求 $\text{[math]}$ 的值；

(2) 求 $\text{[math]}$ 的面积．

综合题普通

3. 如图，一次函数 $\text{[math]}$ 与函数为 $\text{[math]}$ 的图象交于 $\text{[math]}$ 两点．

(1) 求这两个函数的解析式；

(2) 根据图象，直接写出满足 $\text{[math]}$ 时x的取值范围；

(3) 点P在线段 $\text{[math]}$ 上，过点P作x轴的垂线，垂足为M，交函数 $\text{[math]}$ 的图象于点Q，若 $\text{[math]}$ 面积为3，求点P的坐标．

综合题普通