1.
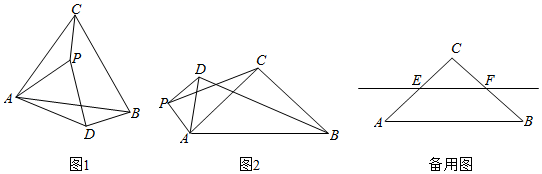
如图1,在  中,∠C=90°,将
中,∠C=90°,将  绕点A逆时针旋转90°得到
绕点A逆时针旋转90°得到  .延长ED分别交CB于点F,交AB于点G,连接AF.
.延长ED分别交CB于点F,交AB于点G,连接AF.
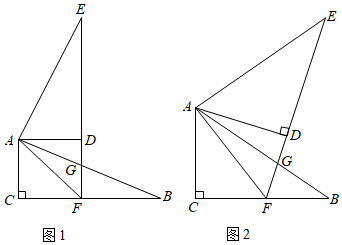
(1)
∠CAF=°,∠EAG=°;
(2)
若BC=(  +1)AC,则①∠DAG= ▲ °;②
+1)AC,则①∠DAG= ▲ °;②  = ▲ , 请证明你的结论;
(3)
如图2,若改变旋转角,已知AC=3,BC=4,当∠EAF=90°时,求
= ▲ , 请证明你的结论;
(3)
如图2,若改变旋转角,已知AC=3,BC=4,当∠EAF=90°时,求  的面积.
的面积.
【考点】
相似三角形的判定与性质;
旋转的性质;
三角形的综合;
能力提升
真题演练