0 返回出卷网首页
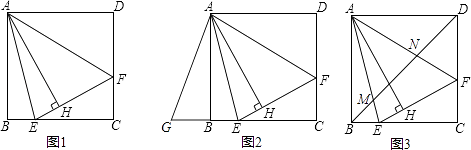
1. 如图，在正方形ABCD中，E为CD边上一点，F为BC延长线上一点，且CE＝CF，连接EF

(1) 若∠FDC＝30°，求∠BEF的度数；
(2) BE与DF之间有怎样的关系？并说明理由
【考点】
正方形的性质; 旋转的性质;
【答案】

您现在未登录，无法查看试题答案与解析。 登录
综合题 普通
能力提升
真题演练
换一批
1. 已知四边形ABCD是正方形，一个等腰直角三角板的一个锐角顶点与A点重合，将此三角板绕A点旋转时，两边分别交直线BC，CD于M，N．

(1) 如图1，当M，N分别在边BC，CD上时，求证：BM+DN=MN
(2) 如图2，当M，N分别在边BC，CD的延长线上时，请直接写出线段BM，DN，MN之间的数量关系
(3) 如图3，直线AN与BC交于P点，MN=10，CN=6，MC=8，求CP的长．
综合题 困难
2. 如图所示，四边形ABCD是正方形，点E是边BC的中点且∠AEF=90°，EF交正方形外角平分线CF于点F，取边AB的中点G，连接EG．

(1) 求证：EG=CF；
(2) 将△ECF绕点E逆时针旋转90°，请在图中直接画出旋转后的图形，并指出旋转后CF与EG的位置关系．
综合题 普通
3. 如图，P是正方形ABCD内一点，△ABP绕着点B旋转后能到达△CBE的位置．

(1) 旋转的角度是多少度？
(2) 若BP=3cm，求线段PE的长．
综合题 普通