0 返回出卷网首页
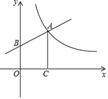
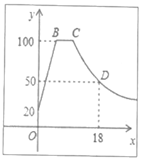
1. 泡茶需要将电热水壶中的水先烧到100℃，然后停止烧水，等水温降低到适合的温度时再泡茶，烧水时水温y(℃)与时间x(min)成一次函数关系；停止加热过了1分钟后，水壶中水的温度y(℃)与时间x(min)近似于反比例函数关系(如图)．已知水壶中水的初始温度是20℃，降温过程中水温不低于20℃．

(1) 分别求出图中所对应的函数关系式，并且写出自变量x的取值范围：
(2) 从水壶中的水烧开(100℃)降到90℃就可以泡茶，问从水烧开到泡茶需要等待多长时间？
【考点】
反比例函数的图象; 反比例函数的性质; 反比例函数的实际应用;
【答案】

您现在未登录，无法查看试题答案与解析。 登录
综合题 困难
能力提升
真题演练
换一批
1. 如图，已知点A在反比例函数 （x＞0）的图像上，过点A作AC⊥x轴，垂足是C，AC=OC．一次函数y=kx+b的图像经过点A，与y轴的正半轴交于点B．

(1) 求点A的坐标；
(2) 若四边形ABOC的面积是 ，求一次函数y=kx+b的表达式．
综合题 普通
2. 如图1，反比例函数y= （x＞0）的图象经过点A（2 ，1），射线AB与反比例函数图象交与另一点B（1，a），射线AC与y轴交于点C，∠BAC=75°，AD⊥y轴，垂足为D．

  

(1) 求k和a的值；
(2) 直线AC的解析式；
(3) 如图3，M是线段AC上方反比例函数图象上一动点，过M作直线l⊥x轴，与AC相交于N，连接CM，求△CMN面积的最大值．
综合题 普通
3. 如图，平行于y轴的直尺(部分)与反比例函数y=  (x>0)的图像交于A，C两点，与x轴交于B，D两点，连接AC，点A、B对应直尺上的刻度分别为5，2。直尺的宽度

BD=2，OB=2．设直线AC的解析式为y=kx+b。

 

(1) 请结合图像直接写出：

①点A的坐标是；

②不等式kx+b> (x>0)的解集是。
(2) 求直线AC的解析。
综合题 普通