1.
如图,⊙O是△ABC的外接圆,BC为⊙O的直径,点E为△ABC的内心(三角形三个内角平分线的交点),连接AE并延长交⊙O于D点,连接BD并延长至F,使得BD=DF,连接CF、BE
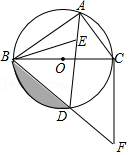
(1)
求证:DB=DE
(2)
求证:直线CF为⊙O的切线
(3)
若CF=4,求图中阴影部分的面积
【考点】
等腰三角形的判定;
切线的判定;
三角形的内切圆与内心;
扇形面积的计算;
三角形的中位线定理;


