如图，在菱形ABCD中，点E在BC边上（与点B、C不重合），连接AE交BD于点G.

0 返回出卷网首页

1. 如图，在菱形ABCD中，点E在BC边上（与点B、C不重合），连接AE交BD于点G.

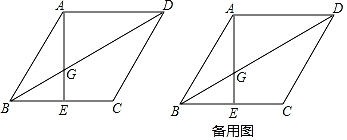
(1) 若AG＝BG，AB＝2，BD＝3，求线段DG的长；

(2) 设BC＝kBE，△BGE的面积为S，△AGD和四边形CDGE的面积分别为S₁和S₂ ，把S₁和S₂分别用k、S的代数式表示；

(3) 求 $\text{[math]}$ 的最大值.

【考点】

二次函数的最值; 三角形的面积; 等腰三角形的性质; 菱形的性质; 相似三角形的判定与性质;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题普通

1. 如图，在 $\text{[math]}$ ABC中，D是BC边上的中点，且AD＝AC，DE⊥BC，DE与AB相交于点E，EC与AD相交于点F.

(1) 说明： $\text{[math]}$ ABC∽ $\text{[math]}$ FCD

(2) 若 $\text{[math]}$ ，BC＝10，求DE的长.

(3) 若 $\text{[math]}$ ，求 $\text{[math]}$ ABC的面积.

综合题困难

2. 已知锐角△ABC中，边BC长为12，高AD长为8

(1) 如图，矩形EFGH的边GH在BC边上，其余两个顶点E、F分别在AB、AC边上，EF交AD于点K

①求 $\text{[math]}$ 的值

②设EH=x，矩形EFGH的面积为S，求S与x的函数关系式，并求S的最大值

(2) 若ABAC，正方形PQMN的两个顶点在△ABC一边上，另两个顶点分别在△ABC的另两边上，直接写出正方形PQMN的边长．

综合题困难

3. 正方形ABCD边长为4，M、N分别是BC、CD上的两个动点，当M点在BC上运动时，保持AM和MN垂直，

(1) 证明：Rt△ABM ∽Rt△MCN；

(2) 设BM=x，梯形ABCN的面积为y，求y与x之间的函数关系式；当M点运动到什么位置时，四边形ABCN的面积最大，并求出最大面积；

(3) 当M点运动到什么位置时Rt△ABM∽Rt△AMN，求此时x的值.

综合题困难