如图，AB为⊙O的弦，若OA⊥OD，AB、OD相交于点C，且CD=BD.

0 返回出卷网首页

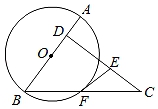
1. 如图，AB为⊙O的弦，若OA⊥OD，AB、OD相交于点C，且CD=BD.

(1) 判定BD与⊙O的位置关系，并证明你的结论；

(2) 当OA=3，OC=1时，求线段BD的长.

【考点】

等腰三角形的性质; 勾股定理; 切线的判定;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题普通

1. 如图，AB是⊙O的弦，OP⊥OA交AB于点P，过点B的直线交OP的延长线于点C，且CP=CB．

(1) 求证：BC是⊙O的切线；

(2) 若⊙O的半径为3，OP=1，求BC的长．

综合题普通

2. 如图，已知直线l与⊙O相离，过圆心O画OA⊥l于点A，交⊙O于点P且OA=5，点B为⊙O上一点BP的延长线交直线l于点C且AB=AC.

(1) 判断AB与⊙O有怎样的位置关系，并说明理由；

(2) 若 $\text{[math]}$ ，求⊙O的半径.

综合题普通

3. 如图，在Rt△ABC中，∠C=90°，点O在AC上，以OA为半径的半圆О交AB于点D，交AC于点E，点F在BC上，且 BF=DF.

(1) 求证：DF是半圆О的切线.

(2) 若AC=4，BC=3，CF=1，求半圆O的半径长.

综合题普通