如图，ΔDBE内接于⊙O，BD为直径，DE＝EB，点C在⊙O（不与D，B，E重合）上，∠A＝45°，点A在直线CD上，连接AB．

0 返回出卷网首页

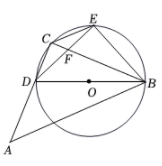
1. 如图，ΔDBE内接于⊙O，BD为直径，DE＝EB，点C在⊙O（不与D，B，E重合）上，∠A＝45°，点A在直线CD上，连接AB．

(1) 如图1，若点C在DE上，求证：ΔABD～ΔCBE；

(2) 在（1）的条件下，DC＝6，DB＝10，求线段CE的长；

(3) 若直线BC与直线DE相交于点F，当 $\text{[math]}$ 时，求 $\text{[math]}$ 的值。

【考点】

勾股定理; 圆周角定理; 圆内接四边形的性质; 相似三角形的判定与性质; 等腰直角三角形;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题困难

1. 如图，⊙O是△ABC的外接圆，AB为直径，CD平分∠ACB交⊙O于点D，OE⊥AC交AC于点E，交CD于点F，连接BD；

(1) 如图1，求∠OFD的度数.

(2) 如图2，过O作OG⊥CD于G，交BC于H，求证：BH=OF；

(3) 如图3，连接BF，若BF=BD，OF=1，求⊙O半径.（画出辅助线，写出简要过程）

综合题困难

2. 如图1，已知△ABC，∠CAB=45°，AB=7，AC= $\text{[math]}$ ， CD⊥AB于点D.E是边BC上的动点，以DE为直径作⊙O，交BC为F，交AB于点G，连结DF，FG.

(1) 求证：∠BCD=∠FDB

(2) 当点E在线段BF上，且△DFG为等腰三角形时，求DG的长.

(3) 如图2，⊙O与CD的另一个交点为P.若射线AP经过点F，求 $\text{[math]}$ 的值.

综合题困难

3. 如图，四边形ABCD为⊙O的内接四边形， AB为⊙O的直径，作DE⊥AB于点E，交AC于点F，其中 $\text{[math]}$ ．

(1) 求证：△ABC∽△DAE.

(2) 当AD= $\text{[math]}$ ， BE=4时，求CD的长.

综合题普通