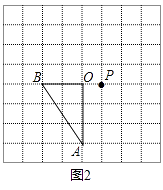
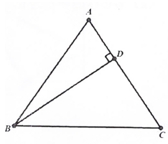
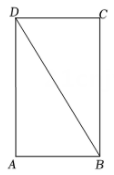
1.
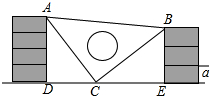
课间,小明拿着老师的等腰三角板玩,不小心掉在两墙之间,如图所示:
(1)
求证: ;
(2)
假设砌墙所用的每块砖块的厚度相同,请你帮小明求出
;
(2)
假设砌墙所用的每块砖块的厚度相同,请你帮小明求出 的值.
的值.
【考点】
锐角三角函数的定义;
三角形全等的判定-AAS;
能力提升
真题演练