0 返回出卷网首页
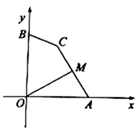
1. 如图，D、E、F分别是△ABC三边中点，AH⊥BC于H．

求证：

(1) ∠BDF＝∠BAC；
(2) DF＝EH．
【考点】
三角形的中位线定理;
【答案】

您现在未登录，无法查看试题答案与解析。 登录
综合题 普通
能力提升
真题演练
换一批
1. 如图，DE是△ABC的中位线，过点C作CF∥BD交DE的延长线于点F．

(1) 求证：DE=EF．
(2) 分别连结DC、AF，若AC=BC，试判断四边形ADCF的形状，并说明理由．
综合题 普通
2. 探索与证明

如图，在△ABC中，BD、CE分别是边AC、AB上的中线，BD与CE相交于点O，M、N分别是BO、CO的中点，顺次连接E、M、N、D四点．

(1) 求证：EMND是平行四边形；
(2) 探索：BC边上的中线是否过点O？为什么？
综合题 普通
3. 如图，已知∠1+∠2=180°，∠3=∠B．


(1) 试判断∠AED与∠ACB的大小关系，并说明你的理由．
(2) 若D、E、F分别是AB、AC、CD边上的中点，S四边形ADFE=4（平方单位），求S△ABC ．

综合题 普通