1.
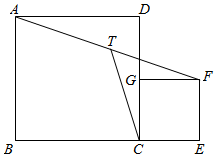
如图,正方形ABCD和正方形CEFG,点G在CD上,AB=5,CE=2,T为AF的中点,求CT的长.
【考点】
勾股定理;
正方形的性质;
直角三角形斜边上的中线;
基础巩固
能力提升
变式训练
拓展培优











