0 返回出卷网首页
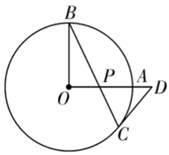
1. 如图，OA和OB是 的半径， ， ，P是OA上任意一点，BP的延长线交 于点C，过点C作 的切线，交OA的延长线于点D.

(1) 求证： ；
(2) 若 ，求PC的长.
【考点】
三角形内角和定理; 等腰三角形的性质; 等边三角形的判定与性质; 切线的性质; 锐角三角函数的定义;
【答案】

您现在未登录，无法查看试题答案与解析。 登录
综合题 普通
能力提升
换一批
1. 已知：AB为⊙O的直径，AB=2，弦DE=1，直线AD与BE相交于点C，弦DE在⊙O上运动且保持长度不变，⊙O的切线DF交BC于点F．

(1)

如图1，若DE∥AB，求证：CF=EF；
(2)

如图2，当点E运动至与点B重合时，试判断CF与BF是否相等，并说明理由．
综合题 困难
2. 如图，AB是⊙O的直径，过点B作⊙O的切线BM，弦CD∥BM，交AB于点F，且= ， 连接AC，AD，延长AD交BM于点E．

(1) 求证：△ACD是等边三角形.
(2) 连接OE，若DE=2，求OE的长.
综合题 普通
3. 在△ABC中，AB=AC，以AB为直径的⊙O分别交边BC、AC于点D、点E，且AE=BE．
(1) 如图①，求∠EBC的度数；

(2) 如图②，过点D作⊙O的切线交AB的延长线于点G，交AC于点F，若⊙O的直径为10，求BG的长．

综合题 普通