如图，在Rt△ABC中，∠ACB=90゜，D为AB的中点，AE//CD，CE//AB，连接DE交AC于点O.

0 返回出卷网首页

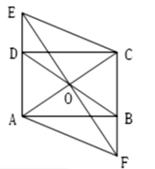
1. 如图，在Rt△ABC中，∠ACB=90゜，D为AB的中点，AE//CD，CE//AB，连接DE交AC于点O.

(1) 证明：四边形ADCE为菱形；

(2) 若∠B=60゜，BC=6，求菱形ADCE的高.

【考点】

等边三角形的判定与性质; 含30°角的直角三角形; 勾股定理; 菱形的判定与性质; 直角三角形斜边上的中线;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题普通

1. 如图， $\text{[math]}$ 中， $\text{[math]}$ ，过点A作 $\text{[math]}$ 的平行线与 $\text{[math]}$ 的平分线交于点D，连接 $\text{[math]}$ ．

(1) 求证：四边形 $\text{[math]}$ 是菱形；

(2) 连接 $\text{[math]}$ 与 $\text{[math]}$ 交于点O，过点D作 $\text{[math]}$ 的延长线交于E点，连接 $\text{[math]}$ ，若 $\text{[math]}$ ， $\text{[math]}$ ，直接写出 $\text{[math]}$ 的长为．

综合题困难

2. 如图，在四边形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，对角线 $\text{[math]}$ ， $\text{[math]}$ 交于点 $\text{[math]}$ ， $\text{[math]}$ 平分 $\text{[math]}$ ，过点 $\text{[math]}$ 作 $\text{[math]}$ 交 $\text{[math]}$ 的延长线于点 $\text{[math]}$ ，连接 $\text{[math]}$ ．

(1) 求证：四边形 $\text{[math]}$ 是菱形；

(2) 若 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的长；

(3) 在（2）的条件下，已知点M是线段 $\text{[math]}$ 上一点，且 $\text{[math]}$ ，则 $\text{[math]}$ 的长为．

综合题普通

3. 如图，在矩形ABCD中，AB=1，对角线AC，BD相交于点O，过点O作EF⊥AC，分别交射线AD与射线CB于点E和点F，连接CE，AF．

(1) 求证：四边形AFCE是菱形．

(2) 当点E，F分别在边AD和BC上时，设AD=x，菱形AFCE的面积是y，求y关于x的函数关系

(3) 当△ODE是等腰三角形时，求AD的长度．

综合题困难