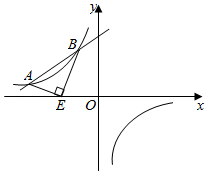
数学模型学习与应用．【学习】如图1，，，于点C，于点E．由，得∠1=∠D；又，可以通过推理得到≌ ．我们把这个数学模型称为“一线三等角”模型；

0 返回出卷网首页

1. 数学模型学习与应用．【学习】如图1， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 于点C， $\text{[math]}$ 于点E．由 $\text{[math]}$ ，得∠1=∠D；又 $\text{[math]}$ ，可以通过推理得到 $\text{[math]}$ ≌ $\text{[math]}$ ．我们把这个数学模型称为“一线三等角”模型；

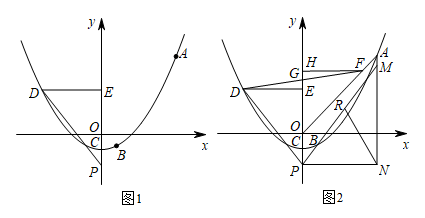
(1) 【应用】如图2，点B，P，D都在直线l上，并且 $\text{[math]}$ ．若 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，用含x的式子表示CD的长；

(2) 【拓展】在 $\text{[math]}$ 中，点D，E分别是边BC，AC上的点，连接AD，DE， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ．若 $\text{[math]}$ 为直角三角形，求CD的长；

(3) 如图3，在平面直角坐标系xOy中，点A的坐标为 $\text{[math]}$ ，点B为平面内任一点． $\text{[math]}$ 是以OA为斜边的等腰直角三角形，试直接写出点B的坐标．

【考点】

三角形全等及其性质; 相似三角形的判定与性质;

【答案】

您现在未登录，无法查看试题答案与解析。登录

实践探究题普通

1. 综合与实践

“手拉手”模型是初中几何图形的一种全等变形的重要模型，可以借助旋转和全等形的相关知识结合勾股定理等，来解决有关线段的长、角的度数等问题，在学习和生活中应用广泛，有着十分重要的地位和作用．

某校数学活动小组进行了有关旋转的系列探究：

如图①，已知 $\text{[math]}$ 和 $\text{[math]}$ 均是等腰直角三角形， $\text{[math]}$ ，且 $\text{[math]}$ ， $\text{[math]}$ ，易证： $\text{[math]}$ ， $\text{[math]}$ ．

(1) 深入探究：

如图②，将图①中 $\text{[math]}$ 绕点A逆时针旋转 $\text{[math]}$ ，连接 $\text{[math]}$ 、 $\text{[math]}$ ，并延长 $\text{[math]}$ 分别与 $\text{[math]}$ 、 $\text{[math]}$ 相交于点 $\text{[math]}$ 、 $\text{[math]}$ ，求证： $\text{[math]}$ ， $\text{[math]}$ ．

(2) 解决问题：

如图③，将图①中 $\text{[math]}$ 绕点 $\text{[math]}$ 逆时针旋转 $\text{[math]}$ ，使 $\text{[math]}$ 与 $\text{[math]}$ 重合，其他条件不变，若 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ ， $\text{[math]}$ ．

(3) 拓展应用：

如图④，将图①中 $\text{[math]}$ 绕点 $\text{[math]}$ 逆时针旋转 $\text{[math]}$ ，连接 $\text{[math]}$ 、 $\text{[math]}$ ，若 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ ， $\text{[math]}$ ．（提示：求 $\text{[math]}$ 时，可过点 $\text{[math]}$ 作 $\text{[math]}$ 于点 $\text{[math]}$ ）