1.
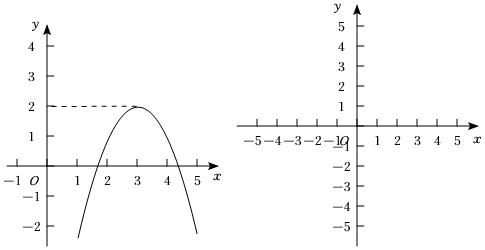
对某一个函数给出如下定义:如果存在实数M,对于任意的函数值y,都满足y≤M,那么称这个函数是有上界函数.在所有满足条件的M中,其最小值称为这个函数的上确界.例如,图中的函数y=﹣(x﹣3)2+2是有上界函数,其上确界是2
(1)
函数①y=x2+2x+1和②y=2x﹣3(x≤2)中是有上界函数的为(只填序号即可),其上确界为;
(2)
如果函数y=﹣x+2(a≤x≤b,b>a)的上确界是b,且这个函数的最小值不超过2a+1,求a的取值范围;
(3)
如果函数y=x2﹣2ax+2(1≤x≤5)是以3为上确界的有上界函数,求实数a的值.
【考点】
一次函数的性质;
二次函数y=ax²+bx+c的性质;