1.
综合与实践
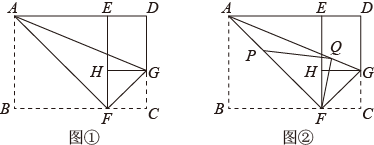
问题情形:如图1,在矩形 中,
,
,点F,G分别在边
,
上,
,
,点E为矩形
的对称中心,连接
,
.易知四边形
为矩形.矩形
保持不动,矩形
绕点C按顺时针方向旋转,旋转角为
.

实践探究:
(1)
如图2,当点E恰好在  上,延长
上,延长  ,交
,交  于点H,则
于点H,则  ;
(2)
如图3,当
;
(2)
如图3,当  的延长线恰好经过点A时,
的延长线恰好经过点A时,  ,
,  分别与
分别与  交于点M,N.则:
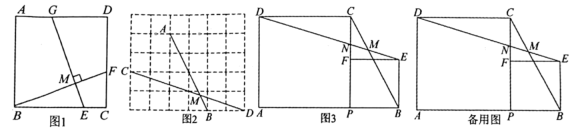
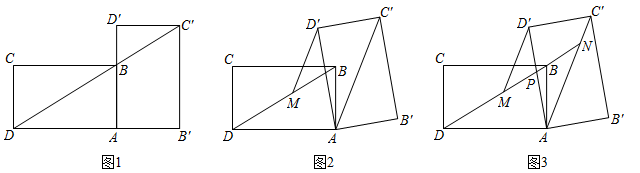
(3)
如图4,若点D在
交于点M,N.则:
(3)
如图4,若点D在  的延长线上,连接
的延长线上,连接  ,
,  .
.
① ;②
;
①此时 ▲ ;
②探究 与
之间的数量关系,并加以证明;
③此时点B,F,E是否在同一条直线上?请说明理由;
④求证: 平分
.
【考点】
矩形的性质;
相似三角形的判定与性质;
四边形的综合;
能力提升
真题演练