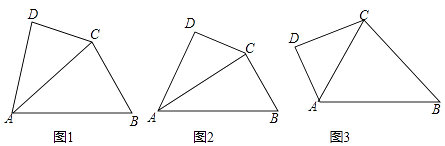
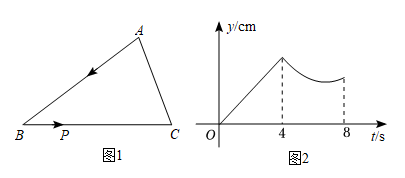
1.
定义:从三角形(不是等腰三角形)的一个顶点引出一条射线与对边相交,顶点与交点所连线段把这个三角形分割成两个小三角形,如果其中一个为等腰三角形,另一个与原三角形相似,我么就把这条线段叫做这个三角形的“华丽分割线”.
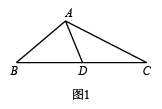
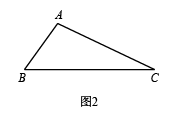
例如:如图1,AD把△ABC分成△ABD和△ADC,若△ABD是等腰三角形,且△ADC∽△BAC,那么AD就是△ABC的“华丽分割线”.
(1)
【定义感知】
(2)
【问题解决】
如图1,在中,
,
AB=BD.求证:AD是
的“华丽分割线”.
①如图2,在中,
, AD是
的“华丽分割线”,且
是等腰三角形,则
的度数是 ▲ ;
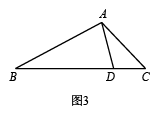
②如图3,在中,AB=2,AC=
, AD是
的“华丽分割线”,且
是以AD为底边的等腰三角形,求华丽分割线AD的长.
【考点】
三角形内角和定理;
等腰三角形的判定与性质;
相似三角形的判定与性质;
能力提升
真题演练