1.
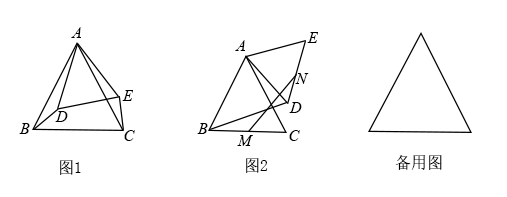
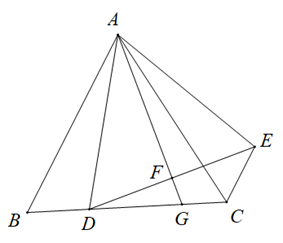
如图,在等边△ABC中,AB=6,D为边BC上一点,以AD为边向右构造等边△ADE,过点A作AF⊥DE于点F,并延长交BC于点G,连接CE.
(1)
求证:BD=CE.
(2)
当  时,求CE的长.
(3)
已知BD=2,
P为边AC的中点,Q为线段AG上一点,当直线PQ将△ACD的面积分成1:3两部分时,求
时,求CE的长.
(3)
已知BD=2,
P为边AC的中点,Q为线段AG上一点,当直线PQ将△ACD的面积分成1:3两部分时,求  的值.
的值.
【考点】
等边三角形的性质;
相似三角形的判定与性质;
锐角三角函数的定义;
三角形全等的判定-SAS;
能力提升
真题演练