1.
如图1,  的面积为1,点
的面积为1,点  ,
,  ,
,  和
和  分别在边
分别在边  ,
,  ,
,  上,
上,  ,
,  ,
,  ,
,  .设
.设  ,图形
,图形  的面积为
的面积为  .
.
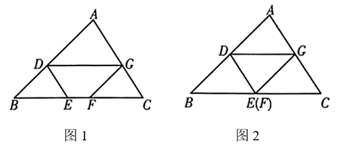
(1)
如图2,当点  和点
和点  重合时,求
重合时,求  与
与  的值;
(2)
如图1,当点
的值;
(2)
如图1,当点  和点
和点  不重合时,求
不重合时,求  的最大值.
的最大值.
【考点】
二次函数的最值;
平行四边形的判定与性质;
相似三角形的判定与性质;